 |
A resistor is a component which
exerts some resistance to the current flowing through it. So this property of
resistor is called its resistance. It is used to reduce the flow of current in
the circuit wherever required. The higher the resistance the lower is the
current allowed through it. Resistance is denoted as ‘R’ and its unit is Ohms or Ω.
 |
Voltage ‘V’, resistance ‘R’ and current ‘I’ is related as R = V/I or I = V/R. So Current is directly proportional to Voltage and inversely proportional to Resistance. So, we get V = I X R, where V is in volts, I in Amperes and R in Ohms. This is called the Ohms law. That means the voltage across a resistance is equal to the current flowing through it multiplied by its
 |
| Resistor Symbol |
Resistor doesn’t have any
polarity; hence any leg of resistor can be connected to any point in circuit.
 |
As I mentioned in Ohms law, the currently is directly proportional the voltage applied across a resistor, means if the voltage is increased the current through resistance also increases and vice-e-versa. If we plot the graph of voltage with respect to resulting current through a resistor, we will get a straight line as shown here.
The slope of the curve is decided by the resistance of the resistor. We have plotted graph for two different resistors here to see difference in behavior. We have drawn a perpendicular line on voltage axis at V=5volts. If we find out at which point the corresponding perpendicular line cuts the current axis, we observer that for red graph its at 1 amps and for the green graph its approx 4 amps. this means the green graph is for a lower resistance and the red graph is for higher resistance.
Series Connection
If two or more resistors are added in series the
total resistance is sum of all resistor values. i.e. R = R1 + R2 + R3 + ….. Rn.
This diagram shows how to connect two or more resistors in series. So in the diagram R1 = 1KΩ
and R2 = 3.3KΩ, so that total resistance is 1 + 3.3 i.e. 4.3KΩ.
 |
Similarly in next diagram total
resistance will be 1 + 1.2 + 3.3 + .220 = 5.72KΩ. Note
here three resistors have value in KΩ and last one in Ω, hence to made same
unit for all, we divided the last resistance value by 1000 to convert from Ω to
KΩ, hence 220Ω/1000 = 0.220KΩ. So we could have converted all three
resistances in KΩ to Ω by multiplying them with 1000 and then adding all to get
the final value in Ω and then we could have divided the final value by 1000 to
get in KΩ.
Let us try that also. R1 = 1KΩ = 1 x 1000Ω
= 1000Ω.
Similarly, R2 = 1.2KΩ = 1.2 x 1000Ω =
1200Ω. R3 = 3.3KΩ = 3.3x1000Ω = 3300Ω, and last one is already in Ω, hence no
change. Now add all four resistance value R = R1 + R2 + R3 + R4 i.e. 1000 +
1200 + 3300 + 220 = 5720Ω. Now finally to get the answer in KΩ divide it by
1000 i.e. R = 5720/1000 = 5.72KΩ.
So we got the same answer as we got earlier. So what we understood that if many
resistors are connected in series the net resistance value increases.
Parallel Connection
Now
let us see how two or more resistors are connected in parallel and what is the net
value of resistance when they are connected so.
So, as the formula shows the net
resistance in case of parallel connection is reciprocal sum of all resistances.
So let us calculate the value of resistance in this case, R = 10 x 10 / (10 +
10) = 100/20 = 5KΩ. So what we observer here is that the net resistance is
lower that individual resistances. Since all resistances in above example are
in KΩ
hence we did straight forward calculation, else we should have made all values
in KΩ
or Ω
either by multiplying or dividing by 1000.
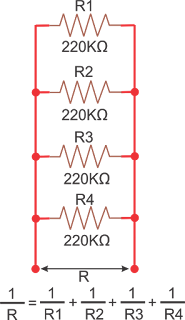In next example on the right we have four
resistor in parallel each with value 220KΩ, so 1/R = (1/220) + (1/220) +
(1/220) + (1/220) = 55KΩ. Again the net value is less that value of any resistance in
parallel circuit. Note: In case of parallel connection the net value will be
less that lowest value of resistance in parallel circuit.Resistor Power Rating
Now when a resistance opposes the
current flowing through it, it does some work to oppose the current which releases
energy from it in the form of heat. Every resistance has another rating that is
its power handling capacity mentioned in “Watts”. The more the wattage of a resistor
the more heat it can dissipate and that means more current it can handle through it. The power developed across a resistor due to current flow in it is calculated
by formula P = V x I i.e. multiplication of voltage across it and the current
flowing through it. Now as we know relation between V, I & R i.e. V = I x R,
now replace V with this value in formula of power, you will get P = I x R X I =
I2 x R and the unit of power is Watts. So, to run a heavy load through resistance, we need high wattage resistor so that it doesn’t over heat and burn
out. For Smaller load we can use low watt resistors.
Next we will learn about Capacitors, keep watching.
0 Comments